服务器4线风扇接口定义以及转速读取机制

一般服务器或交换机上的风扇接口都会走以下几种信号：

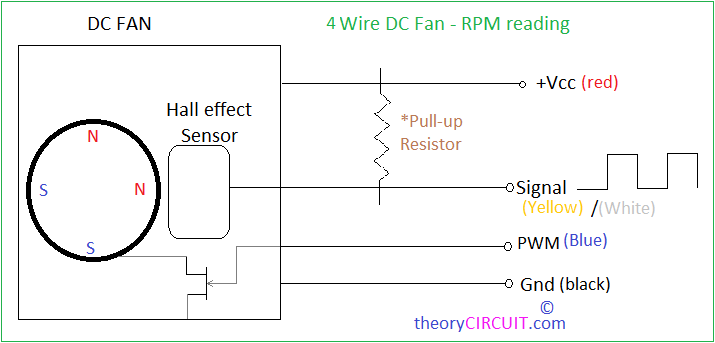
TACH（Tachometer）信号，转速表的意思，一些说明书里也被称为FG（Frequency Generator）信号。注意TACH是开集电极输出，需要上拉电阻。

TACH信号输出的是一个频率可变的方波信号。其原理是，在风扇转子旁边布置了一个霍尔传感器，当电机转动的时候，电机的转子的磁体经过霍尔传感器时，输出一个高电平，经过信号处理后输出一个方波。因为转子转一圈一般会输出2个方波信号，因此方波的2个周期的时间就是电机转子转动一圈的时长。因此，电机转速 rpm = Freq_方波 * 60/2 ，单位为 rad/min 。

在实际检测电路中，定义常量 N_puls 表示风扇每转一圈产生脉冲个数，一般为2；定义一个测量时间窗 T_mea （例如500ms）；设置一个计数器 M（例如8bit），用于统计时间窗内收到的脉冲数； 那么风扇转速为： rpm = M * 60/(T_mea * N_puls) ，单位为 rad/min 。因为计数器 M 存在最大值，如果风扇的满转速过高，需要配置减小测量的时间窗以匹配。

小工具集合

基于项目 smilelc3/MyLittleTool 和 smilelc3/sudoku-solver，并使用 wasm 技术实现 JavaScript 调用 C/C++ 和 Go。

Linear11 格式转换实数

提交

输出:

Linear16 格式转换实数

提交

输出:

某些题目，由于要计算的答案非常大（超出64位整数的范围），会要求把答案对 10⁹ + 7取模。如果在计算中途没有处理得当的话，会出现WA（错误）或则TLE（超时）。

例如计算多项乘积时，如果没有中途及时取模，乘法结果会溢出（例如C/C++），从而得到非预期的答案 。对于 Python 来说，虽然没有溢出，但是大整数（big integer）之间的运算不是 O(1)，可能会导致LTE。

加法和乘法的取模

一般涉及到取模（$\bmod$）的题目，会用到如下两个恒等式 $$ \begin{align} (a+b) \bmod m &= ((a \bmod m) + (b \bmod m)) \bmod m \\ (a \cdot b) \bmod m &= ((a \bmod m) \cdot (b \bmod m)) \bmod m \\ \end{align} $$

证明：根据带余除法，∀a ∈ 𝕫，都可以表示为a = qm + r (m ≠ 0)，其中整数q为a除以m的商（quotient），整数r为a除以m的余数（remainder），即r = a mod  m。

设a = q₁m + r₁，b = q₂m + r₂。 第一个恒等式： $$ \begin{align} (a+b) \bmod m &= (q_1 m + r_1 +q_2 m + r_2) \bmod m \\ &=((q_1 + q_2)m + r_1 + r_2) \bmod m \\ &=(r_1 + r_2) \bmod m \end{align} $$ 又因为r₁ = a mod  m，r₂ = b mod  m有： (a + b) mod  m = ((a mod  m) + (b mod  m)) mod  m

第二个恒等式： $$ \begin{align} (a\cdot b) \bmod m &= ((q_1 m + r_1)(q_2 m + r_2)) \bmod m \\ &= (q_1 q_2 m^2 + (q_1 r_2 + q_2 r_1)m + r_1 r_2) \bmod m \\ &=(r_1 r_2) \bmod m \end{align} $$

同样有： (a ⋅ b) mod  m = ((a mod  m) ⋅ (a mod  m)) mod  m

根据这两个恒等式，我们可以在计算过程中（例如循环中），对加法和乘法的结果取模，而不是在计算最终结果后再取模。

注意：如果涉及到幂运算，不能随意取模。如果指数为整数，可以用快速幂。

如果计算过程中有减法，可能会产生负数，处理不当也会导致 WA。如何正确处理这种情况呢？

同余

首先引入同余（congruence modulo） 的概念。 两个整数a，b，若它们除以正整数m所得的余数相等，则称a，b对于模m同余，记作： a ≡ b (mod  m)

例如42 ≡ 12 (mod  10)，因为42和12都可以被10整除，余数都是2。

负数的取模

对于负数，我们可以将其转化为对应的非负数再取模。例如，−17 mod  10可以转化为((−17 mod  10) + 10) mod  10 = (−7 + 10) mod  10，结果是3。 也就是说，如果我们发现 (x mod  m) < 0，可以加上一个m，得到非负数。

为避免判断x mod  m < 0，可以写成 (x mod  m + m) mod  m

这样无论x是否为负数，运算结果都会落在区间[0, m − 1]中。

除法的取模

如果要计算$\frac{24}{8} \bmod 5$，如果像加法或乘法处理，写成$\frac{24 \bmod 5}{8 \bmod 5} \bmod 5 = \frac{4}{3}$，明显不是正确答案3。先有结论：

如果p是一个质数，a是b的倍数且b和p互质，那么有 $$ \frac{a}{b} \bmod p = (a \cdot b^{p-2}) \bmod p $$

如果实际题目中推导出了包含除法的求余式，可以用上式转换成乘法，并用快速幂计算b^p − 2 mod  p。

证明：

• 引理1： 当p是质数且1 ≤ i ≤ p − 1时，有 C_pⁱ ≡ 0 (mod  p)

其中 $$ \mathrm{C}_p^i = \frac{p!}{i!(p-i)!} $$ 证明：当p是质数且1 ≤ i ≤ p − 1时，$\frac{p!}{i!(p-i)!}$分母一定不含p，由于分子中包含p且C_pⁱ为整数，所以C_pⁱ一定能被p整除，即C_pⁱ ≡ 0 (mod  p)。

• 引理2： 根据二项式定理，有 $$ (x+y)^p = \sum_{k=0}^{p}{\mathrm{C}_p^k x^{p-k} y^k} = \sum_{k=0}^{p}{\mathrm{C}_p^k x^k y^{p-k}} $$

当p为质数，且x, y ∈ 𝕫时，除去k = 0和k = p两项，根据引理1，其余项与0关于p同余。即 $$ \sum_{k=1}^{p-1}{\mathrm{C}_p^k x^{p-k} y^k} \equiv 0 \pmod p $$ 拆分 $$ \begin{align} (x+y)^p &= \mathrm{C}_p^0 x^p y^0 + \sum_{k=1}^{p-1}{\mathrm{C}_p^k x^{n-k} y^k} + \mathrm{C}_p^p x^0 y^p \\ &=x^p + y^p + \sum_{k=1}^{p-1}{\mathrm{C}_p^k x^{n-k} y^k} \end{align} $$

于是当p为质数，且x, y ∈ 𝕫时，有： (x + y)^p ≡ x^p + y^p (mod  p)

根据费马小定律，对任意整数a和任意质数p，有： a^p ≡ a (mod  p) 证明：当a = 0时，0^p ≡ 0 (mod  p)成立； 已知引理2，通过归纳法，我们可以得到： (x₁ + ... + x_n)^p ≡ x₁^p + ... + x_n^p (mod  p)

如果将a展开为a个1相加，a = 1 + ... + 1,代入上式有： a^p ≡ (1 + ... + 1)^p ≡ 1^p + ... + 1^p ≡ a (mod  p)

根据数学归纳法，原命题对于 a ≥ 0 成立。对于a < 0的情况同理，证明完毕。

如果a不是p的倍数，费马小定理也可以写成更加常用的一种形式： a^p − 1 ≡ 1 (mod  p) 如果a是p的倍数，显然有：a^p − 1 ≡ 0 (mod  p)。

在a不是p的倍数的前提下，两边同时乘以$\frac{b}{a}$，有 $$ b \cdot a^{p-2} \equiv \frac{b}{a} \pmod p $$

即 $$ \frac{b}{a} \bmod p = (b \cdot a^{p-2}) \bmod p $$

总结

1
2
3
4
5
6
7
8
9

// 如果取模到 [0, MOD-1] 中，无论正负
(a % MOD + MOD) % MOD

// 多个数相乘，要步步取模，防止溢出
(a * b * c) % MOD = a * b % MOD * c % MOD

// 除（MOD 是质数且 b 不是 MOD 的倍数）
(a / b) % MOD =  a * qpow(b, MOD-2, MOD) % MOD  // qpow 是快速幂

RTL8367S自制网管交换机

RTL8367S 芯片官网介绍

RTL8367S-CG

二层管理 5+2 端口 10/100/1000M 交换机控制器

概述

RTL8367S-CG 是一款 LQFP-128 封装的高性能 5+2 端口 10/100/1000M 以太网交换机，具有低功耗集成 5 端口 Giga-PHY，支持 1000Base-T、100Base-TX 和 10Base-T传输标准。

对于特定应用，RTL8367S 支持一个额外的接口，可配置为 RGMII/MII 接口。 RTL8367S 还支持一个可配置为 SGMII/HSGMII 接口的 Ser-Des 接口。 RTL8367S集成了高速交换机系统的所有功能；包括用于数据包缓冲的 SRAM、无阻塞交换结构以及单个 CMOS 器件中的内部寄存器管理。

特点

单芯片 5+2 端口 10/100/1000M 无阻塞交换架构

嵌入式 5 端口 10/100/1000Base-T PHY

每个端口支持全双工 10/100/1000M 连接（半双工仅在 10/100M 模式下支持）

额外接口（扩展 GMAC1）支持

SGMII (1.25GHz) 接口

HSGMII (3.125GHz) 接口

额外接口（扩展GMAC2）支持

媒体独立接口 (MII)

简化的 10/100/1000M 媒体独立接口 (RGMII)

通过 IEEE 802.3x 流量控制和背压进行全双工和半双工操作

应用

5 端口 1000Base-T 路由器，带 SGMII/HSGMII 和/或 MII/RGMII

芯片官网介绍：https://www.realtek.com/Product/Index?id=3699

RTL8367S-CG_Datasheet.pdf¹

原理图

外围电路

1. 使用 USB-C 输出5V电源
2. 使用 SY8088IAAC 实现 5V 降压 3.3V，使用RTL8367S自带电压转换输出1.1V
3. 使用 W25Q32JVSSIQ 4MB spi norflash 存储固件
4. 使用 5个 HR911130A 自带变压器和 LED 的单端口RJ45连接器
5. 转出 TX/RX 串口
6. 带 3.3V 供电拉低按钮 + 芯片重置按钮
7. 25M 晶振时钟

3D效果图

固件

借用网件GE105Ev2的固件

https://www.netgear.com/cn/business/wired/switches/plus/gs105ev2/

网件固件.bin，大小2M。

使用烧录器（例如CH341）烧写到 spi norflash中。

修改mac地址

固件MAC地址固定为00:00:00:00:00:01，编辑固件中偏移地址 0x1FC000指定MAC地址，可以随机生成MAC